https://www.acsysteme.com/wp-content/uploads/2021/07/PID-forme-parallele-16x9-1.jpg
PID série ou parallèle, quelle structure choisir ?
Introduction
Au niveau du codage et de la mise en œuvre de ce type de régulateur, une question nous a récemment été posée par un client : faut-il utiliser la forme PID série ou la forme PID parallèle ? En effet, lors de nos premiers cours d’automatique, le professeur nous apprend qu’il existe deux formes de PID, mais il ne nous précise pas dans quel contexte il faut préférer l’une des formes à l’autre.
1. PID série ou parallèle
Ces deux formes sont décrites pas les équations ci-dessous :
- PID série :
Cserie(s) = k(1+1⁄(sτi) )(1+sτd)
- PID parallèle :
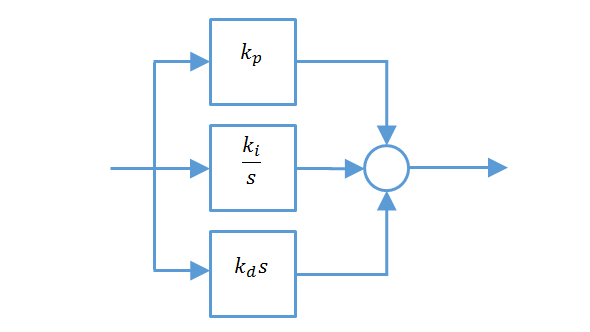
Cparallele(s) = kp + ki ⁄s + kds
Ce qui est important de remarquer, c’est que ces deux formes sont mathématiquement équivalentes. Ainsi un régulateur sous forme série pourra être mis sous forme parallèle à partir des équations de transformation suivante :
- kp = k(1 + τd ⁄τi )
- ki = k⁄ τi
- kd = kτd
https://www.acsysteme.com/wp-content/uploads/2021/07/PID-forme-serie.jpg
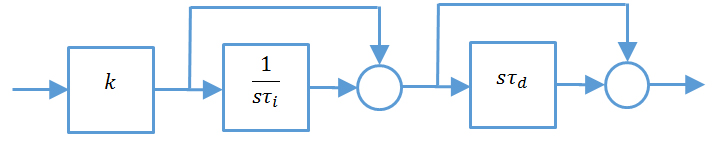
Fig 1 : PID forme série
https://www.acsysteme.com/wp-content/uploads/2021/07/PID-forme-parallele-16×9-1.jpg
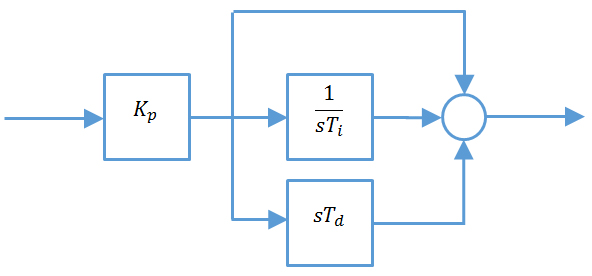
Fig 2 : PID forme parallèle
2. Une 3ème forme de PID
Une 3ème forme de PID existe ! Celle-ci est appelée « standard », « mixte » ou parfois « idéal ». Elle est définie par l’équation ci-dessous [1]:
Cstandard(s) = Kp(1 + 1⁄sΤi + sΤd )
Cette forme standard se rapproche beaucoup de la forme parallèle et les équations de transformation entre les deux sont évidentes. La transformation de la forme série en forme standard s’obtient par les équations suivantes :
Kp = k(1 + τd ⁄τi )
Τi = τi + τd
Τd = τdτi ⁄(τd + τi)
Il existe donc trois formes différentes des mises en œuvre des régulateurs PID et ces trois formes sont presque mathématiquement équivalentes. Dans la plupart des cas (à l’exception par exemple de ki=0), il existe des formules pour transformer un régulateur d’une forme vers une autre forme.
https://www.acsysteme.com/wp-content/uploads/2021/07/PID-forme-standard.jpg
3. La principale différence
La principale différence entre ces différentes formes concerne l’effet des coefficients de réglage sur le comportement du régulateur. Ainsi la forme parallèle permet de découpler complètement les actions proportionnelle, intégrale et dérivée entre elles. Alors que dans la forme standard, une modification sur la valeur du coefficient Kp va modifier simultanément les actions proportionnelle, intégrale et dérivée. À ce titre, certaines personnes, qui règlent des PID de manière manuelle, préfèrent la forme parallèle.
La forme série se trouve parfois dans certains automates de régulation du marché. Il existe une 2nde formulation de la forme série [2]:
Cserie(s) = (1+τ1)(1+τ2)⁄τi(1+τNs)
Cette formulation permet de facilement mettre en relation les constantes de temps du procédé avec les paramètres de réglage du régulateur et notamment les deux zéros réels du numérateur.
Dans l’industrie, les formes standard et parallèle sont les plus courantes. Ainsi dans le logiciel Simulink, le bloc « PID Controller » propose les formes standard (« Ideal ») et parallèle (« Parallel »).
Un autre point important à remarquer est que les formes série et standard ne permettent pas l’annulation de l’action intégrale et donc la transformation d’un régulateur de type PID en régulateur de type PD.
https://www.acsysteme.com/wp-content/uploads/2021/07/ressource-PID-Simulink-PID-Controller-750×625.png
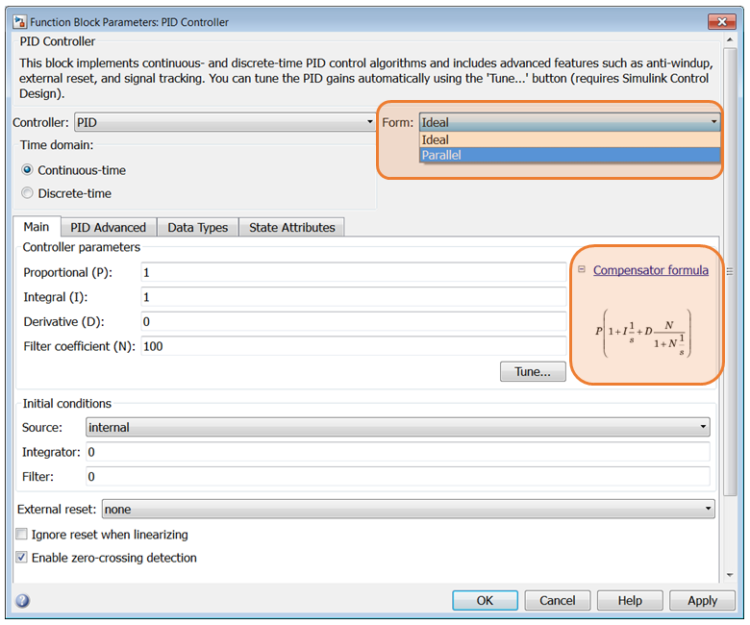
Menu du « PID Controller » sous Simulink
4. Conclusion
En conclusion, il est difficile de préconiser une forme particulière pour la mise en œuvre des régulateurs PID, chacune présentant des avantages et des inconvénients. La forme standard est la plus utilisée dans l’industrie. Il est important de savoir que toutes ces formes sont finalement très similaires et qu’il existe des formules pour passer d’une forme à l’autre. Les différences portent principalement sur l’effet des paramètres de réglage sur le comportement de la boucle de régulation ce qui s’avère fondamental dans le cadre de la mise au point manuelle.
Si malgré tout, vous hésitez encore, les conseillers d’Acsystème se tiennent à votre disposition pour vous aider à analyser vos besoins et à faire les bons choix. Vous pouvez nous contacter par ce formulaire : Nous contacter.
Sébastien SALIOU, mai 2014
Références bibliographiques :
[1] Philippe de Larminat, Automatique appliquée, 2e édition revue et augmentée, Chapitre 2, Hermès Lavoisier, 2009.
[2] A. Besançon-Voda et S. Gentil, Régulateurs PID analogiques et numériques, Techniques de l’ingénieur, R 7 416, mars 1999.