Automatique et épidémie de Covid-19
Steve Brunton, a brillamment relevé ce défi dans une série de 4 vidéos pédagogiques. Il a fait le parallèle entre la théorie de l’automatique et les stratégies de contrôle de l’épidémie.
Le but de l’automatique est de trouver un contrôleur qui permet de maitriser l’évolution d’une ou plusieurs grandeurs d’un système en respectant une consigne.
Dans le cas d’une épidémie :
- le système est l’épidémie,
- la grandeur peut être le nombre de personnes en soins intensifs, le nombre de personnes infectées, ou encore le nombre de décès par exemple,
- la consigne peut être de rester en dessous de la capacité hospitalière, minimiser le nombre de décès ou encore minimiser le nombre de personnes infectées,
- le contrôleur est l’ensemble des mesures prises par le gouvernement (confinement, masques, distanciation sociale, fermeture des bars et restaurants…) et que nous appliquons plus ou moins bien.
Pour concevoir le contrôleur et valider son fonctionnement, l’automaticien a besoin de modéliser son système. La modélisation d’une épidémie est très complexe, car elle fait intervenir des notions sociétales et psychologiques. Les êtres humains ont des comportements hétérogènes, qui peuvent évoluer au fil du temps en fonction de plusieurs paramètres comme la météo par exemple. De plus, tous les virus ne se comportent pas de la même manière.
Par conséquent, la modélisation nécessite de faire des hypothèses. Steve Brunton, montre une comparaison de plusieurs modèles de l’évolution du nombre de morts en fonction du temps. Cette comparaison issue d’un article du New York Times montre clairement que chaque prévision contient une marge d’erreur relativement importante et qu’elles sont différentes les unes des autres (Figure 1). Aucun des modèles n’est parfait et leurs paramètres sont bien souvent incertains, néanmoins ils restent très utiles pour concevoir la stratégie de contrôle et évaluer sa robustesse.
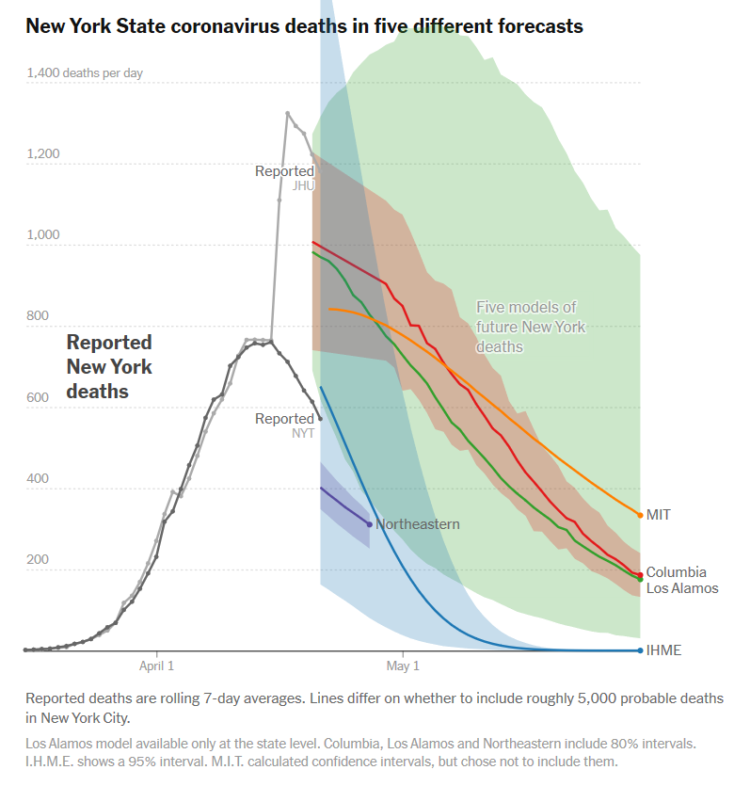
Figure 1 : 5 modèles qui donnent des prévisions qui sont très dispersées et très différentes les unes des autres (Graphique issue de l’article « What 5 Coronavirus Models Say the Next Month Will Look Like » écrit par Quoctrung Bui, Josh Katz, Alicia Parlapiano et Margot Sanger-Katz, paru le 22/04/2020 sur le site de The New York Times).
Parmi les grandes familles de modèles citées, les modèles compartimentaux (type SIR) permettent de décrire l’évolution de l’épidémie par des équations différentielles. Le nombre de reproduction de base (nommé R0) est un des principaux paramètres qui agit sur cette évolution. Ce nombre indique le nombre moyen qu’une personne contagieuse peut infecter. Les mesures sanitaires agissent donc principalement sur ce paramètre. Une autre famille de modèle est constituée par les modèles statistiques qui sont purement mathématiques et dont les paramètres sont identifiés sur la base d’observations (de mesures).
Une fois que la dynamique de l’évolution de l’épidémie est comprise et que le modèle est établi, il est temps de réfléchir à la stratégie de contrôle. Il est maintenant admis, que sans stratégie de contrôle, l’épidémie va croitre exponentiellement et devient vite incontrôlable. C’est une situation que veulent éviter la plupart des gouvernements. D’où l’importance d’adopter une stratégie de contrôle.
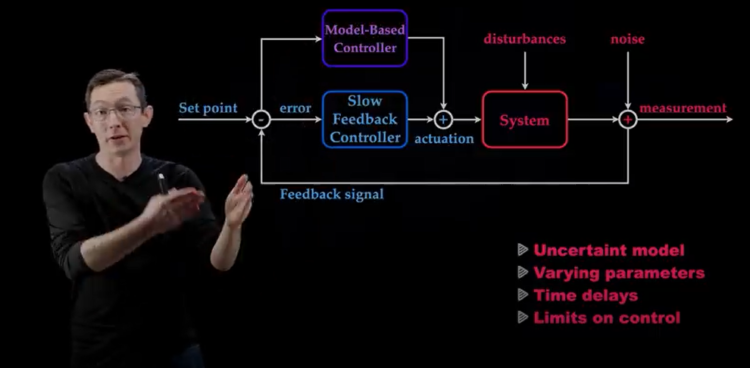
En automatique, la boucle fermée est une structure de contrôle classique. Elle consiste à piloter un système via un contrôleur qui reçoit comme information l’erreur entre la consigne (l’objectif fixé) et la mesure de la grandeur d’intérêt du système. Une stratégie de contrôle en boucle fermée serait donc de comparer le nombre de patients admis en soins intensifs avec la capacité hospitalière et d’ajuster les mesures (confinement, masques, …) en conséquence. Le cœur de l’automatique est ici, quel algorithme va nous permettre de déterminer le bon niveau de mesures de distanciation sociale au bon moment pour atteindre le plus rapidement notre objectif en respectant les contraintes.
La « mesure » est aussi ici très importante, car elle va avoir un impact sur les performances du contrôleur. Il est par exemple, préférable de contrôler le nombre de patients admis à l’hôpital ou en soins intensifs car la mesure est beaucoup plus précise que le nombre de personnes infectées car tout le monde n’est pas testé.
La stratégie de contrôle peut être vouée à l’échec si la notion de robustesse n’est pas prise en compte. Le modèle utilisé étant imparfait, les paramètres incertains et des perturbations (évènements climatiques, rassemblements non prévus ou encore émeutes) peuvent s’appliquer sur le système. De plus, les retards présents dans le système épidémique du COVID 19 peuvent fortement limiter la robustesse du contrôle. Ces retards sont de différentes natures, on peut citer par exemple, le retard entre le moment où les décisions sont prises et le moment où elles sont appliquées ou encore le retard lié au temps d’incubation. La mise au point des stratégies de contrôle doit donc être menée avec soin afin de vérifier que le contrôleur permet de stabiliser le système de manière sûre et robuste.
Pour contrôler ce type de système, Steve Brunton propose d’utiliser le MPC (model predictive control). Cet algorithme consiste à prédire, via un modèle, le comportement du système sur un horizon donné et choisir la commande qui permet de respecter la consigne sur cet horizon, tout en minimisant l’effort de contrôle. Ce processus est répété à chaque itération. Comme les modèles sont imparfaits et qu’il y a des retards, le MPC est couplé avec un régulateur en boucle fermé qui va comparer la consigne avec l’état du système actuel mesuré et donc corriger si nécessaire la commande.
Toutes les notions et techniques abordées sur cette série de vidéos sont utilisées quotidiennement par les ingénieurs d’Acsystème qui ont vocation à modéliser des systèmes et créer des algorithmes qui permettent de les contrôler. Même si nous avons plutôt l’habitude de les appliquer aux domaines des transports, de l’énergie ou de l’industrie, le champ d’application est bien plus large. Comme nous venons de le voir, elles peuvent être appliquées à d’autre domaines comme celui de la santé publique.
Marouane Benaziz, juin 2020
Sources :
- Control Theory and COVID-19 by Steve Brunton https://www.youtube.com/watch?v=BTLZu-1IMcE
- Quoctrung Bui, Josh Katz, Alicia Parlapiano et Margot Sanger-Katz, What 5 Coronavirus Models Say the Next Mont Will Look Like, publié sur le site du New York Times, le 22/04/2020 : https://www.nytimes.com/interactive/2020/04/22/upshot/coronavirus-models.html
